Die verfügbaren statischen und dynamischen Berechnungsmöglichkeiten erlauben die Analyse rotierender Systeme, welche besonderen Randbedingungen unterworfen sind.

Statik

In einer quasistatischen Berechnung, die z.B. auch den Kontakt im Nabenbereich berücksichtigt, werden die Zentrifugalkräfte aufgrund der Drehung berücksichtigt. Dabei ist das Bezugssystem ein mitrotierendes Relativsystem oder das Inertialsystem (bei axialsymmetrischem Rotor). Die statische Berechnung ist auf den unterkritischen Betrieb beschränkt.

In einer linearen Berechnung werden die Zentrifugalfeldsteifigkeit und die geometrische Steifigkeit jeweils bei der angegebenen Drehzahl berücksichtigt. Bei einer geometrisch nichtlinearen Berechnung erfolgt eine Korrektur der Zentrifugalkräfte.

Dynamik

Um den Verlauf der Eigenfrequenzen über der Drehzahl zu ermitteln steht ein automatisches Verfahren zur Verfügung, mit dem ein Campbell-Diagramm direkt erstellt werden kann.

In der Dynamik rotierender Systeme geht man von den allgemeinen Voraussetzungen einer linearisierten Bewegungsgleichung mit konstanten Koeffizienten aus. Das Bezugssystem kann ein mitrotierendes Relativsystem oder das Inertialsystem sein. Die Drehgeschwindigkeit wird als konstant vorausgesetzt.

Bei einer Kopplung von rotierenden und nicht-rotierenden Teilen im mitdrehenden Bezugssystem muss man für den rotierenden Teil keinerlei Einschränkung berücksichtigen, während die nicht-rotierenden Teile eine isotrope Lagerung für den Rotor darstellen müssen.

Für diese Konfiguration können die direkten und modalen Methoden im Zeit- und Frequenzbereich eingesetzt werden. Dabei wird auch die jeweilige Coriolis-Matrix bei der Lösung berücksichtigt.

Bei einer Dynamik im Inertialsystem hat man für die nicht-rotierende Struktur keine weiteren Einschränkungen zu berücksichtigen, aber die rotierende Struktur muss axialsymmetrisch sein.

Auch für diese Konfiguration können die direkten und modalen Methoden im Zeit- und Frequenzbereich unter Berücksichtigung der Kreiselmatrix eingesetzt werden. Dabei bleiben die modalen Methoden zur Ermittlung der dynamischen Antwort auch im überkritischen Bereich einsetzbar.

Um die kritische Drehgeschwindigkeit zu ermitteln, kann ein Campbell-Diagramm verwendet werden. Im mitdrehenden Bezugssystem wird ein Eigenwert bei der kritischen Geschwindigkeit einen Nullwert zeigen.

Eine drehzahlabhängige Steifigkeit und viskose Dämpfung von Rotorlagern kann in einer komplexen Eigenwertanalyse und bei der Erstellung eines Campbell-Diagramms berücksichtigt werden. Das wird mit einem speziellen Element erreicht.

Von speziellem Interesse bei der Dynamik ist die stationäre Antwort im Modalraum. Dabei werden zunächst die statischen Spannungen unter Zentrifugallast ermittelt. Dann werden geometrische und Zentrifugalfeldsteifigkeit einbezogen und die Verschiebungen für den konstanten Lastanteil berechnet. Nach einer Eigenwertanalyse werden im Modalraum dann Frequenzgänge für jede Harmonische ermittelt, welche dann nach einer Rücktransformation in den physikalischen Raum mit den statischen Verschiebungen im Zeitbereich überlagert werden.

Änderung des Schwingungsverhaltens einer Tischkreissäge beim Hochlauf.

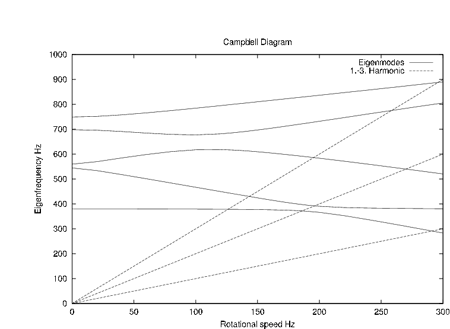
Campbell-Diagramm für die Auswertung in der Rotordynamik


Einen Flyer zu diesem Thema finden Sie hier.