Berechnung von Werkzeugmaschinen mit PERMAS
Alle verfügbaren dynamischen Analysemethoden können auch für die Berechnung von Werkzeugmschinen verwendet werden, wie die Eigenwert- und Frequenzganganalyse, die komplexe Eigenwertberechnung und die Zeitintegration. Außerdem stehen Optimierungsverfahren zur Verfügung, um Modelländerungen zu ermitteln, welche die Eigenschaften einer Werkzeugmaschine bezüglich Gewicht und unter statischer dynamischer Belastung verbessern können.
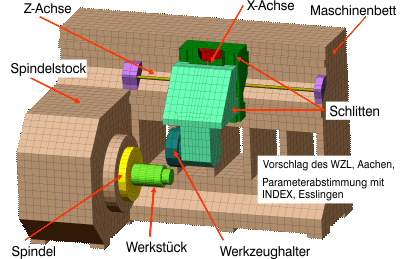
Einfaches Modell einer Drehmaschine
Modell
Die folgenden typischen Maschinenteile wurden für das Modell herangezogen:
- Bauteile: Maschinenbett, Schlitten und Spindelstock werden als Volumenmodell erstellt.
- Führungen: Diese sind Bestandteil der Struktur, aber die passende Modellierung der Verbíndung geschieht über Feder-Dämpfer-Systeme, wobei die Feder- und Dämpferkräfte mit den verbundenen Volumenstrukturen über geeignete MPC-Bedingungen unter Berücksichtigung von inkompatiblen Netzen gekoppelt werden.
- Kugelgewindetriebe: Diese werden mit Balkenelementen modelliert. Ihre Funktion besteht darin, die Drehbewegung des Antriebs in eine translatorische Bewegung des Schlittens umzusetzen. Diese Transformation wird mit Hilfe einer MPC-Bedingung realisiert, welche den Durchmesser des Gewindes und seine Steigung berücksichtigt.
- Spindel mit Werkstück: Spindel und Werkstück werden wieder als Volumenmodelle realisiert. Die Kopplung zum Spindelstock erfolgt über ein spezielles Element und wieder mit einer geeigneten MPC-Bedingung. Das spezielle Element wird benötigt, um Steifigkeit und Dämpfung der Spindel-Lagerung abhängig von der Drehgeschwindigkeit zu gestalten.
- Regelung: Um die Regelung im Modell zu berücksichtigen, wurde ein finites Element entwickelt,
das einen sog. Kaskadenregler darstellt.
Dieser Kaskadenregler enthält Positions- und Geschwindigkeitsregler zusammen mit
Filtern und einem Stromregler. Dieser Regler enthält alle typischen Regelungsanteile,
wie sie für die Regelung von Werkzeugmaschinen gebraucht werden und er wurde in
Kooperation mit Herstellern von Werkzeugmaschinen entwickelt.
Die Aktuatorkraft wird als Moment in den Kugelgewindetrieb beider angetriebener Achsen eingespeist (Z-Achse und X-Achse). Die Sensoren für die relativen Positionsänderungen befinden sich zwischen dem Maschinenbett und dem Z-Schlitten bzw. zwischen dem Z-Schlitten und dem X-Schlitten. Die Sensoren für die relative Geschwindigkeit (mit Hilfe von Drehratensensoren) befinden sich an den Kugelgewindetrieben.
Die Parameter des Reglers müssen den tatsächlichen Regler wiedergeben, wie er in der Maschine verbaut wird. Deshalb sind die Parameter dem Berechnungsingenieur als Eingangswerte zur Verfügung zu stellen (wie auch andere Werte, z.B. fürs Material). Damit ist der Berechnungsingenieur in der Lage, die Entwicklung der Maschine mit einer vollen Systemsimulation zu unterstützen.
Im Beispielmodell befinden sich zwei Regler, einer für die translatorische Bewegung parallel zur Spindelachse (Z-Achse) und einer für die radiale Bewegung (der Werkzeugzustellung, X-Achse). Die Reglerparameter sind in beiden Fällen weitgehend dieselben.
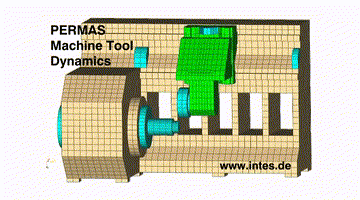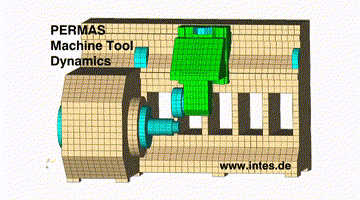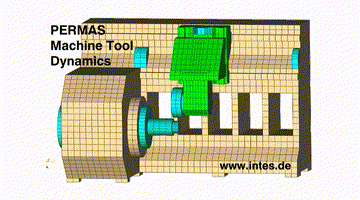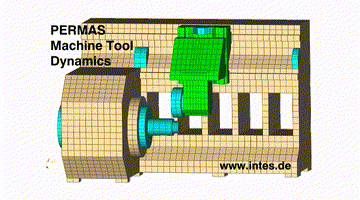
Systemantwort auf einen plötzlichen Positionssprung
Berechnung
Typische Methoden zur dynamischen Berechnung von Werkzeugmaschinen sind:
- Eigenwertanalyse: Modale Methoden haben den Vorteil, dass sie wegen der Modellreduktion deutlich effizienter sind. Trotzdem stehen auch direkte Verfahren zur Verfügung.
- Modale Frequenzganganalyse: Der Frequenzgang für Amplitude und Phase zwischen Werkzeug und Werkstück bei einer bestimmten Anregung unter ungeregelten und geregelten Bedingungen kann berechnet werden.
- Modale Zeitintegration: Die Antwort auf eine Positionsänderung des
Werkzeugs kann ermittelt werden. Die Positionsänderung kann sprunghaft
oder als glatter Übergang (wie eine Sinusfunktion) gestaltet werden.
Dabei kann auch die Rotation der Spindel berücksichtigt werden.
Zusätzlich ist es wichtig zu erwähnen, dass die nichtlinearen Lagerbedingungen der Spindel in der modalen Zeitintegration verwendet werden können. - Komplexe Eigenwertanalyse: Die Wirkung der Systemdämpfung (wie in den Führungen und im Spindellager) sowie die dämpfende Wirkung der Regelung auf die Verlagerung der Eigenfrequenzen kann mit der komplexen Eigenwertanalyse ermittelt werden (unter Berücksichtigung der Kreiseleffekte). Damit ist auch eine Stabilitätsbetrachtung des Reglers möglich.
- Stabilitätsanalyse des Prozesses: Für die Entwicklung einer Werkzeugmaschine ist es besonders wichtig, schon
früh eine Aussage über auftretende Instabilitäten machen zu können. Es ist
das Ziel der Entwicklung, eine Maschine zu bekommen, die stabil mit hoher
Genauigkeit bei hoher Geschwindigkeit arbeitet. Die Quelle von Instabilitäten
liegt in der Interaktion zwischen Werkzeug und Werkstück, wobei die Energie
der selbsterregten Schwingungen aus der rotierenden Spindel kommt.
Um den nichtlinearen Drehprozess berechenbar zu machen, wurde ein Schnittkraftmodell entwickelt. Dieses hängt von der Schnittgeschwindigkeit, der Schnitttiefe und der Zustellung pro Umdrehung ab. Das Schnittkraftmodell erfordert eine Reihe von Koeffizienten, die sich auf die Kombination eines bestimmten Werkzeugs mit einem bestimmten Material des Werkstücks beziehen. Diese Koeffizienten müssen über einige Experimente mit dieser Kombination ermittelt und kalibriert werden.
Damit können eine Stabilitätskarte erstellt und die zugehörigen Ratterfrequenzen ermittelt werden. Dabei kann ein besonders wichtiger Effekt der Spindeldrehung beobachtet werden. Die Stabilität hängt von der Drehrichtung der Spindel ab. Bei diesem Beispiel erlaubt die Links-Drehung (gegen den Uhrzeigersinn) höhere Schnitttiefen als die Rechts-Drehung (im Uhrzeigersinn) der Spindel.
Mit einer Zeitintegration für einen Arbeitspunkt (bei 1300 U/min) zeigt sich, dass ein stabiles Verhalten bei Linksdrehung und ein instabiles Verhalten bei Rechtsdrehung auftritt.

Komplexer Eigenmode
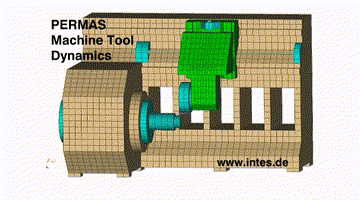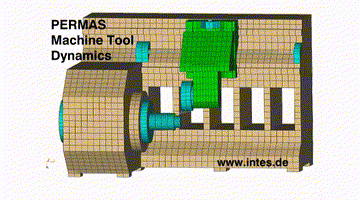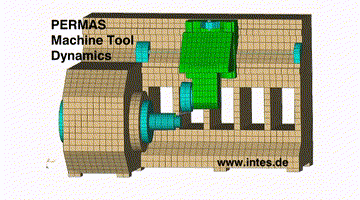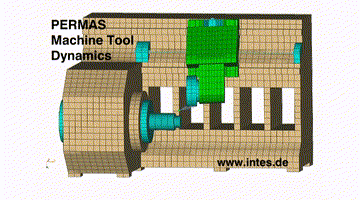
Instabiles Verhalten bei rechtsdrehender Bearbeitung
Optimierung
Einige Anwendungsbeispiele für den Einsatz der Optimierung können noch ergänzt werden:
- Die Topologie-Optimierung kann verwendet werden, um leichtere Werkzeugmaschinen zu erhalten. Dabei können Regler und weitere dynamische Bedingungen berücksichtigt werden (wie Eigenfrequenzen, Frequenzgang).
- Formoptimierung, um die richtigen Aufstandspunkte der Maschine zu ermitteln.
- Optimierung der Reglerparameter, um Eigenfrequenzen zu verschieben und den Frequenzgang zu verbessern.
Nehmen Sie mit uns Kontakt auf!
INTES Ingenieurgesellschaft für technische Software mbH
Geschäftsführer: Rolf Fischer
Breitwiesenstr. 28
70565 Stuttgart
Handelsreg.: Stuttgart HRB 10 978
USt-Ident-Nr.: DE 147803245
Tel.: +49 711 78499-0
✉info@intes.de