Dynamic Eigenvalues
The PERMAS-DEV (Dynamics/Eigenvalues) module provides for the calculation of real eigenvalues and mode shapes of the structure (eigenvalue analysis). The specification of a number of modes and an upper frequency limit is supported. The very efficient subspace iteration algorithm used is capable of solving very large eigenvalue problems. Rigid body modes are detected automatically or may be explicitly defined and are decoupled prior to the subspace iteration.
Shift method
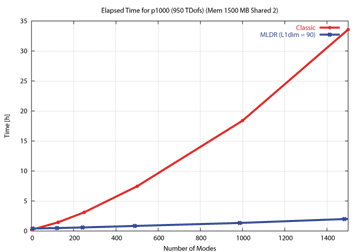
If the number of modes is increasing, one can observe a disproportional increase of solution time, because the last modes take more time than the first modes. Therefore, a shift method has been introduced which are used to split the frequency domain in several parts and to solve each part separately. Then, even the last modes can be solved as fast as the firstmodes resulting in an overall run time reduction for the complete analysis. The shift method is used automatically by PERMAS in cases where a large number of modes is required (> 5000 modes) or where the standard method takes a long time to converge. In addition, a higher accuracy of the mode shapes can be expected from this method. For very large models, the MLDR method is recommended.
The stiffness matrix can be modified taking into account additional stiffness effects:
- Geometric stiffness for any load,
- Centrifugal stiffness for rotating parts under constant rotational speed referring to co-rotating reference system,
- Convective stiffness for rotating parts under constant rotational speed referring to inertial reference system,
- Pressure stiffness for shell elements and fluidfilled pipe elements under pressure.
Additional tools are available for the further processing of modes:
- Modal stresses can be derived from modal displacements.
- In addition, modal potential and kinematic energies can be calculated and exported.
- For the evaluation of modes, e.g. with respect to local or global mode shapes, energy balances can be determined and exported for all sets in a structure.
- MAC (Modal Assurance Criterion) factors and other factors are available to compare modes between two different modal analyses
- As a measure for the completeness of the modal model, effective masses are generated and printed on the result file.
A generalized modal condensation is available to establish system matrices in modal space for external applications. Export of modal models is either supported by interfaces (e.g. to MBS systems) or by direct specification of the matrix items.
The modal basis is very efficient to compute responses like random response. See DRA.
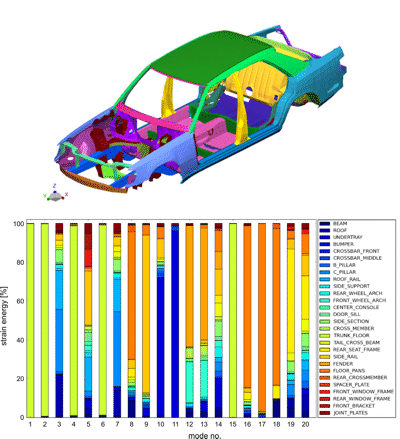
Strain energy distribution over all body parts (same color in the model)
for the first 20 eigenmodes.
Extended Mode Analysis
- Dynamic condensation
- Complex mode analysis
- Eigenfrequencies over rotational speed for rotating structures
Dynamic Condensation
Two methods are available for dynamic condensation:
- Craig-Bampton method (CB condensation),
- Mixed-Boundary Craig Bampton method(MBCB condensation).
Craig Bampton method
The Craig-Bampton method uses fixed-interface vibration modes and the static deflections due to unit displacements of the interface degrees of freedom for the dynamic reduction of substructures (CB condensation). Like for the Guyans reduction, an explicit and an iterative scheme is available in order to achieve good performance.The functionality comprises:
- Structural dynamics
- Acoustics
- Coupled fluid-structure acoustics
Two condensation options are available for coupled fluid-structure acoustics:
- Dry Interface
- Solution of a coupled eigenvalue problem on subcomponent level, i.e. isolation of the acoustic component. External modes are coupled modes.
- Global solution may be a mechanical vibration analysis.
- Wet Interface
- Separate computation of mechanical and acoustic modes on subcomponent level.
- Global solution is a coupled vibration analysis.
- Condensation of the fluid-structure interface can also be made.
Mixed-Boundary Craig Bampton method
The method allows for free (or mixed) boundary conditions to derive the vibration modes (MBCB condensation). The corresponding static deflections are derived using inertia relief. This method is advantageous when the condensation is used for structures with free boundaries, because the condensation method can represent the boundary conditions. In such cases, less number of required modes and a higher accuracy can be expected from the Mixed-Boundary Craig-Bampton method compared to the classical Craig-Bampton method.The above mentioned dry condensation of parts with enclosed fluids also works with the Mixed-Boundary Craig-Bampton method.
Complex Mode Analysis
This includes the calculation of complex eigenvalues and eigenvectors in modal coordinates. This method is based
on a previous solution of the real eigenvalue task.
The results of this analysis are as follows:
- Frequency
- Complex eigenvalues
- Complex eigenfrequencies (damping coefficient and circular frequency)
- Equivalent viscous damping ratio
- Complex mode shapes with physical and modal representation. The modal displacements of the complex modes represent the modal participation of the underlying real modes.
A suitable post-processor (like VisPER) can be used to visualize and animate complex mode shapes.
Eigenfrequencies of Rotating Systems
For rotational systems it is often required to generate a so-called Campbell diagram, which relates the eigenfrequencies to the rotational speed. The values of such a diagram can be generated automatically in one single run. From these values all frequencies of interest can be selected for a subsequent frequency response analysis.
For rotating structures, any number of rotational speeds is defined in a separate input. A reference rotational velocity is used in the static pre-run. From this pre-run, additional matrices are built for the reference rotational velocity. The specified rotational velocities are used to scale the additional matrices during dynamic response analysis. This procedure makes the generation of Campbell diagrams very efficient and the response analysis of rotating structures is facilitated.
Eigenmodes with automated substructuring (MLDR)
This benefit in elapsed run time can be essentially raised more, if there is a subsequent dynamic response analysis calculating the response behavior just at a small number of nodes. Then, the generation of the global mode shapes can be saved resulting in considerable computing time savings.
The MLDR method is based on an automatic partitioning of the model where each part does not exceed a preset quantity. In addition, the coupling between the parts has to be as low as possible. These parts are then groupwise combined as substructures using dynamic condensation. This procedure is hierarchically carried on until the complete model is represented in one component. In this component only a small number of nodes and elements remain and the dynamic behavior is mainly determined by the modes and frequencies taken over from the substructrues and combined following the rules of dynamic condensation. Due to this procedure the method's name is Multi-Level Dynamic Reduction (MLDR)
If certain nodes and elements should be present in the main component, the user can specify them explicitly. So, selected model parts can be pushed to the main component and any subsequent processing of the modes is rather beneficial due to the small size of the remaining matrix system. In this way, dynamic simulation, coupling to MBS, optimization of the remaining system, or the consideration of nonlinearities can be performed with very low computing times.
Additional reductions of computing time are possible using multi-processor systems, because the method has been fully parallelized. Altogether, the use of MLDR is a big step forward to more productivity and allows, for example, dynamic simulation in a higher frequency range as in the past together with a possible increase in model size for more accurate results.