Dynamik (Eigenwerte)
Das Modul PERMAS-DEV (Dynamik Eigenwerte und -vektoren) ermöglicht die Berechnung von reellen Eigenwerten und Eigenformen der Struktur. Zur Eingrenzung des berechneten Frequenzbereichs kann eine Anzahl von Eigenformen oder eine obere Frequenzschranke angegeben werden. Der hierfür verwendete, sehr effiziente Algorithmus zur Unterraumiteration ist zur Lösung selbst größter Eigenwertaufgaben geeignet. Starrköpereigenformen werden automatisch gefunden oder können auch explizit definiert werden. In jedem Fall werden sie vor der Eigenwertanalyse entkoppelt.
Shift-Methode
Mit steigender Anzahl von Moden beobachtet man eine überproportionale Zunahme der Rechenzeit für die Eigenwertanalyse, weil die letzten Moden mehr Zeit benötigen als die ersten. Deshalb wurde eine Shift-Methode eingeführt, um den Frequenzbereich in mehrere Teile aufzuteilen und jeden Teil für sich zu lösen. Damit können die letzten Moden genauso schnell ermittelt werden wie die ersten, was insgesamt zu einer Laufzeitreduktion führt. Die Shift-Methode wird automatisch verwendet, wenn eine große Anzahl von Moden gesucht wird (> 5000) oder wenn die Standardmethode zu lange für das Erreichen der Konvergenz benötigt. Außerdem sorgt die Shift-Methode für eine verbesserte Genauigkeit der Eigenformen. Für sehr große Modelle empfiehlt sich MLDR
Die Steifigkeitsmatrix kann vor einer Eigenwertberechnung durch zusätzliche Effekte modifiziert werden:
- Geometrische Steifigkeit für beliebige Belastungen,
- Zentrifugalfeldsteifigkeit für rotierende Bauteile unter konstanter Drehgewschwindigkeit in einem mitrotierenden Bezugssystem,
- Konvektive Steifigkeit für rotierende Bauteile unter konstanter Drehgeschwindigkeit in einem Inertialsystem,
- Drucksteifigkeit für Schalenelemente und flüssigkeitsgefüllte Rohrelemente unter Druckbelastung.
Für die weitere Bearbeitung von Eigenformen stehen zusätzliche Hilfsmittel zur Verfügung:
- Aus den Verschiebungsformen der Eigenformen können modale Spannungen abgeleitet werden.
- Außerdem können modale potentielle und kinetische Energien berechnet und ausgegeben werden.
- Zur Bewertung der Eigenformen z.B. hinsichtlich lokaler oder globaler Eigenformen können Energiebilanzen über alle Sets einer Struktur ermittelt und ausgegeben werden.
- Zum Vergleich der Eigenformen aus verschiedenen Eigenwertanalysen können MAC-Faktoren (Modal Assurance Criterion) und weitere Faktoren berechnet und ausgegeben werden.
- Zur Beurteilung der Vollständigkeit eines modalen Modells eignen sich effektive Massen, die in geeigneter Weise auf der Ergebnis-Datei ausgegeben werden.
Eine verallgemeinerte modale Kondensation ermöglicht den Aufbau aller erforderlichen Systemmatrizen im Modalraum, um die Berechnung außerhalb von PERMAS durchzuführen. Der Export dieser Matrizen wird entweder durch spezielle Schnittstellen (z.B. zu MKS-Systemen) durchgeführt oder durch explizite Angabe der auszugebenden Matrizen.
Die modale Basis ist für viele Antwortverfahren sehr effizient, wie z.B. zufallserregte Schwingungen. Siehe DRA.
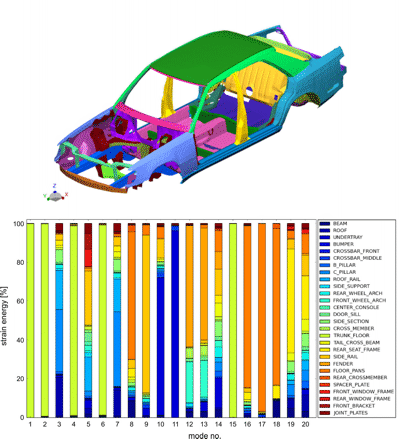
Verteilung der Dehungsenergie auf die Bauteile (gleiche Farbe im Modell)
für die ersten 20 Eigenformen.
Erweiterte Eigenwertanalyse
- Dynamische Kondensation
- Komplexe Eigenwertberechnung
- Eigenwertverlauf über Drehzahlbereich für drehende Systeme
Dynamische Kondensation
Zwei Verfahren stehen für die dynamische Kondensation zur Verfügung:
- Verfahren nach Craig-Bampton (CB-Kondensation)
- Verfahren nach Craig-Bampton mit gemischten Randbedingungen (MBCB-Kondensation)
Craig-Bampton-Verfahren
Das Verfahren von Craig-Bampton verwendet die Eigenschwingungsformen von Teilstrukturen bei festgehaltenem Rand und zusätzliche statische Verschiebungsformen aufgrund von Einheitsverschiebungen am Rand der Teilstrukturen (CBKondensation). Wie für die statische Kondensation stehen auch hier explizite und iterative Verfahren für die Kondensation zur Verfügung, um kurze Rechenzeiten sicherzustellen.Die bereitgestellt Funktionalität umfasst:
- Strukturdynamik
- Akustik
- gekoppelte Fluid-Struktur Akustik
Zwei Optionen stehen für die Kondensation bei der gekoppelten Fluid-Struktur Akustik zur Verfügung:
- Trockene Kopplung
- Lösung des gekoppelten Eigenwertproblems für eine Teilkomponente, d.h. das Fluid wird von der Teilkomponente eingeschlossen und keine Druckfreiheitsgrade koppeln nach außen. Somit sind die externen Moden der Teilkomponente selbst gekoppelte Moden.
- Die Gesamtlösung kann damit eine reine Strukturschwingungsanalyse sein.
- Benetzte Kopplung
- Die mechanischen und akustischen Moden werden in getrennten Teilkomponenten berechnet.
- Die Gesamtlösung ist somit selbst eine gekoppelte Fluid-Struktur-Berechnung.
- Dies erfordert eine zusätzliche Kondensation der Koppelelemente zwischen Fluid und Struktur.
Craig-Bampton-Verfahren mit gemischen Randbedingungen
Das Craig-Bampton-Verfahren mit gemischten Randbedingungen erlaubt auch freie (oder gemischte)Randbedingungen zur Ermittlung der Schwingungsmoden (Mixed-Boundary Craig-Bampton, MBCB-Kondensation). Die entsprechenden statischen Verschiebungen werden über eine quasistatische Analyse(d.h. Inertia Relief) ermittelt. Dieses Verfahren hat Vorteile für Strukturen, die freie Randbedingungen haben, weil die Kondensation mit entsprechenden Randbedingungen arbeiten kann. Dabei können weniger Moden zu einer höheren Genauigkeit des kondensierten Systems führen verglichen mit dem klassischen Verfahren.Die oben beschriebene trockene Kondensation von Teilen mit eingeschlossenen Fluiden kann auch mit dem Craig-Bampton-Verfahren mit gemischten Randbedingungen durchgeführt werden.
Komplexe Eigenwertanalyse
Dies umfasst die Berechnung komplexer Eigenwerte und Eigenvektoren im Modalraum. Das verwendete Verfahren basiert auf
einer zuvor durchgeführten Berechnung der reellen Eigenwerte.
Die damit ermittelten Ergebnisse sind wie folgt:
- Frequenz
- Komplexe Eigenwerte
- Komplexe Eigenfrequenzen (mit Kreisfrequenz und Dämpfung)
- Äquivalentes viskoses Dämpfungsverhältnis
- Komplexe Eigenformen in physikalischer und modaler Darstellung. Die modalen Verschiebungen der komplexen Eigenformen stellen die modalen Anteile der zu Grunde liegenden reellen Eigenformen dar.
Mit einem geeigneten Postprozessor (wie VisPER) können die komplexen Eigenformen auch animiert dargestellt werden.
Eigenwerte rotierender Systeme
Für rotierende Systeme stellt sich oft die Aufgabe, den Verlauf der Eigenfrequenzen über der Drehzahl darzustellen (in einem Campbell-Diagramm). Dieser Verlauf lässt sich in einem einzigen Rechenlauf automatisch erstellen. Damit können die interessanten Punkte für eine nachfolgende Frequenzgangberechnung einfach ermittelt werden.
Für rotierende Strukturen kann eine beliebige Anzahl von Drehgeschwindigkeiten in einer eigenen Eingabe spezifiziert werden. Eine Referenzgeschwindigkeit wird in einem statischen Vorlauf verwendet, um die erforderlichen Zusatzmatrizen zu ermitteln. Diese werden dann mit jeweiligen Drehgeschwindigkeiten skaliert. Damit wird die Erstellung von Campbell-Diagrammen sehr effizient und die Berechnung des Antwortverhaltens drehender Strukturen erleichtert.
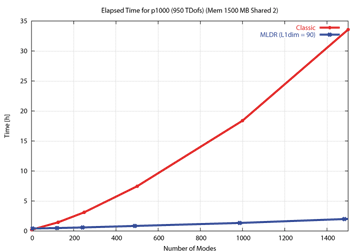
Eigenwerte mit automatischer Unterstrukturtechnik (MLDR)
Dieser Laufzeitvorteil kann sich noch erheblich steigern, wenn der Eigenwertanalyse eine dynamische Simulation folgt, bei der es auf Frequenzgänge oder Zeitverläufe nur einiger relativ weniger Knoten ankommt. In diesen Fällen kann die Ermittlung der globalen Moden für alle Freiheitsgrade unterbleiben, was einen erheblichen Rechenzeitgewinn bedeutet.
Die MLDR-Methode basiert darauf, dass das Modell automatisch in Teile aufgespaltet wird, die eine gewisse vorgegebene Größe nicht überschreiten. Dabei wird auf eine geringe Kopplung dieser Teile untereinander geachtet. Diese Teile werden dann als Teilstrukturen durch Anwendung der dynamischen Kondensation gruppenweise zusammengefasst. Dieses Verfahren wird hierarchisch solange fortgesetzt, bis die Gesamtstruktur in einer Komponente repräsentiert ist. Dabei verbleiben lediglich eine Reihe von Knoten und Elementen in der Hauptkomponente und das dynamische Verhalten wird vor allem durch die von den Teilstrukturen übernommenen Eigenfrequenzen und Eigenformen bestimmt, welche nach den Regeln der dynamischen Kondensation verbunden werden. Diesem mehrstufigen dynamischen Reduktionsverfahren verdankt die Methode ihren Namen MLDR (Multi-Level Dynamic Reduction).
Sollen ganz bestimmte Knoten und Elemente in der Hauptkomponente präsent sein, so kann dies der Anwender direkt angeben. Damit können ausgesuchte Modellteile in die Hauptkomponente gezwungen werden, was die weitere Verarbeitung der Moden auf einem relativ kleinen System sehr vorteilhaft gestaltet. So lassen sich anschließend dynamische Simulation, Anbindung an MKS, Optimierung auf dem verbleibenden System oder die Einbindung von Nichtlinearitäten mit äußerst niedrigen Rechenzeiten realisieren.
Da die Methode vollständig parallelisiert ist, können weitere Rechenzeitvorteile durch die Nutzung von Mehrprozessormaschinen erzielt werden. Insgesamt ist daher mit dem Einsatz von MLDR ein wesentlicher Fortschritt in der Produktivität verbunden und erlaubt somit z.B. auch Berechnungen bis in einen höheren Frequenzbereich hinein als vorher und dies auch mit feineren Netzen.