Analyse dynamique modale
Le module PERMAS-DEV détermine les valeurs propres réelles et les déformées modales d'une structure. Le choix du nombre de modes et/ou d'une fréquence limite est possible. PERMAS utilise un algorithme très efficace d'itérations sur un sous-espace, capable de résoudre de très gros problèmes aux valeurs propres. Les modes de corps rigides, détectés automatiquement ou définis de façon explicite, sont découplés avant les itérations sur le sous-espace.
Shift method
If the number of modes is increasing, one can observe a disproportional increase of solution time, because the last modes take more time than the first modes. Therefore, a shift method has been introduced which are used to split the frequency domain in several parts and to solve each part separately. Then, even the last modes can be solved as fast as the firstmodes resulting in an overall run time reduction for the complete analysis. The shift method is used automatically by PERMAS in cases where a large number of modes is required (> 5000 modes) or where the standard method takes a long time to converge. In addition, a higher accuracy of the mode shapes can be expected from this method. For very large models, the MLDR method is recommended.
The stiffness matrix can be modified taking into account additional stiffness effects:
- Geometric stiffness for any load,
- Centrifugal stiffness for rotating parts under constant rotational speed referring to co-rotating reference system,
- Convective stiffness for rotating parts under constant rotational speed referring to inertial reference system,
- Pressure stiffness for shell elements and fluidfilled pipe elements under pressure.
Résultats additionnels:
- Contraintes modales, déterminées à partir des déplacements modaux,
- Energies modales potentielles et cinétiques,
- Répartition des énergies par groupes d'éléments pour évaluer un comportement local ou global du mode,
- Coefficients href="https://en.wikipedia.org/wiki/Finite_element_updating">MACs (Modal Assurance Criterion) et autres critères pour comparer des bases modales.
- Masses effectives, crées systématiquement, pour mesurer la complétude de la base modale et caractériser les modes.
A generalized modal condensation is available to establish system matrices in modal space for external applications. Export of modal models is either supported by interfaces (e.g. to MBS systems) or by direct specification of the matrix items.
The modal basis is very efficient to compute responses like random response. See DRA.
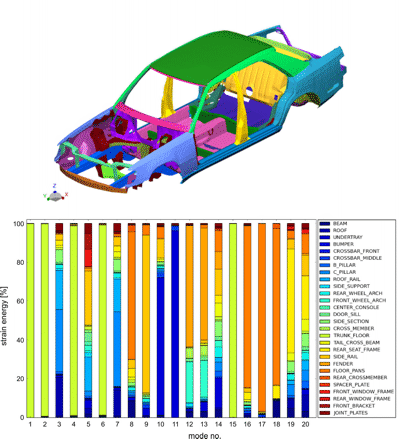
Strain energy distribution over all body parts (same color in the model)
for the first 20 eigenmodes.
Analyse modale étendue
- Condensation dynamique
- Analyse modale complexe
- Fréquences propres en fonction de le vitesse de rotation pour les structures tournantes
Condensation dynamique
Two methods are available for dynamic condensation:
- Craig-Bampton method (CB condensation),
- Mixed-Boundary Craig Bampton method(MBCB condensation).
Craig Bampton method
The Craig-Bampton method uses fixed-interface vibration modes and the static deflections due to unit displacements of the interface degrees of freedom for the dynamic reduction of substructures (CB condensation). Like for the Guyans reduction, an explicit and an iterative scheme is available in order to achieve good performance.The functionality comprises:
- Dynamique des structures
- Acoustique
- Couplage fluide structure
Deux options de condensation sont possibles pour le couplage fluide structure:
- Interface "sèche"
- Solution du problème couplé aux valeurs propres au niveau du sous-composant, i.e. isolation de la partie fluide. Les modes externes sont des modes couplés.
- Solution globale issue d'une analyse dynamique modale classique de structure sèche.
- Interface "mouillée"
- Détermination des modes structures et des modes acoustiques au niveau du sous-composant.
- Solution globale issue d'une analyse dynamique modale couplée.
- Les points de condensation peuvent contenir de degès de liberté de type pression.
Mixed-Boundary Craig Bampton method
The method allows for free (or mixed) boundary conditions to derive the vibration modes (MBCB condensation). The corresponding static deflections are derived using inertia relief. This method is advantageous when the condensation is used for structures with free boundaries, because the condensation method can represent the boundary conditions. In such cases, less number of required modes and a higher accuracy can be expected from the Mixed-Boundary Craig-Bampton method compared to the classical Craig-Bampton method.The above mentioned dry condensation of parts with enclosed fluids also works with the Mixed-Boundary Craig-Bampton method.
Analyse modale complexe
Cette fonctionnalité permet le calcul de valeurs et de vecteurs propres complexes en coordonnées modales. Cette méthode est basée sur un calcul préalable de valeurs propres réelles. Les résultats d'une telle analyse sont les suivants:
- Fréquences
- Valeurs propres complexes
- Fréquences propres complexes (coefficient d'amortissement et pulsation)
- Coefficient d'amortissement réduit équivalent
- Déformées des modes complexes avec une représentation physique et modale. Les déplacements modaux des modes complexes représentent les participations modales des modes réels associés.
La visualisation et l'animation des déformées de modes complexes sont possibles avec un post-traitement graphique adapté (comme VisPER).
Fréquences propres des systèmes en rotation
Pour les systèmes en rotation, la génération du diagramme dit "de Campbell" qui relie les fréquences propres avec la vitesse de rotation est souvent nécessaire. Les valeurs de ce diagramme sont déterminées automatiquement avec un seul calcul. A partir de ces résultats, les fréquences intéressantes sont sélectionnées pour une analyse consécutive en réponse fréquentielle.
For rotating structures, any number of rotational speeds is defined in a separate input. A reference rotational velocity is used in the static pre-run. From this pre-run, additional matrices are built for the reference rotational velocity. The specified rotational velocities are used to scale the additional matrices during dynamic response analysis. This procedure makes the generation of Campbell diagrams very efficient and the response analysis of rotating structures is facilitated.
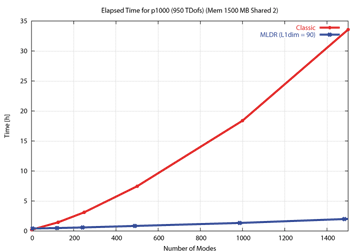
Analyse modale avec MLDR
Ce bénéfice en terme de temps de calculs peut être nettement amélioré si une réponse dynamique consécutive est utilisée pour déterminer la réponse sur un petit nombre de nœuds seulement. En effet, la génération complète des déformées modales est évitée, économisant ainsi des temps de calcul considérables.
La méthode MLDR est basée sur une partition automatique du modèle où chaque partition ne dépasse pas une taille donnée. De plus, le couplage entre les différentes partitions doit être le plus faible possible. Ces partitions sont alors regroupées et organisées comme des sous-structures en utilisant la condensation dynamique. Cette procédure est appliquée sur plusieurs niveaux de manière hiérarchique afin de représenter le modèle complet par un seul composant. Dans ce composant, seulement un petit nombre de nœuds et d'éléments est conservé et le comportement dynamique est principalement déterminé par les modes et les fréquences issus des sous-structures et combinés en suivant les règles de la condensation dynamique. En raison de cette procédure, cette méthode de condensation dynamique à plusieurs niveaux est appelée MLDR (Multi-Level Dynamic Reduction).
Si des nœuds et des éléments particuliers doivent être présents dans le composant principal, l'utilisateur peut les spécifier directement. Ainsi, la partie sélectionnée du modèle est placée dans le composant principal, et tous les traitements consécutifs sur les modes sont alors accélérés étant donné la petite taille matricielle du système résultant. De cette façon, les simulations en dynamique, les couplages avec la cinématique, l'optimisation du système résultant, ou la prise en compte de non-linéarités peuvent être traités avec des temps de calculs très faibles.
Comme cette méthode est complètement parallélisée, il est possible de réduire davantage les temps de calculs en utilisant des machines multi-processeurs. En conclusion, l'utilisation de MLDR est une avancée importante dans l'augmentation de la productivité, et permet, par exemple, la simulation dynamique dans des plages de fréquences plus élevées que celles étudiées par le passé, avec la possibilité d'augmenter la taille des modèles pour ameliorer la precision des resultats.