Reliability Analysis/Robust Design Optimization
Reliability Analysis
In contrast to this method, the stochastic analysis of a design assumes some properties of a structure or the loads to be uncertain knowing only the characteristics of their probability distributions. The limiting constraints on the design will usually be of the same kind as in the deterministic approach. However, the results from the probabilistic analysis will yield the probability of failure with respect to these constraints and the sensitivity of this probability with respect to the uncertain properties of the model.
This module combines the Finite Element Analysis with the well known COMREL software developed by RCP GmbH, Munich. So, the experience comprised in both software systems could be merged in a single application simplifying the approach to the Stochastic Finite Element Method.
Reliability analysis steps:
- Definition of uncertain quantities in structural analysis (like geometrical or load parameters) by basic variables with an assigned distribution function.
- Definition of limit state functions (or failure functions) related to result quantities of a structural analysis.
- Calculation of the probability of failure for each limit state function.
Basic variables:
- Design parameters (like geometrical data or coordinates)
- Load factors
- Material parameters
- Parameters of the limit state functions
- Parameters of other basic variables
More than 20 different types of distribution functions are available to describe the basic uncertain variables.
Available analysis types:
- Linear static analysis
- Contact analysis
- Dynamic eigenvalue analysis
Available methods:
- Efficient sensitivity based methods as First/Second Order Reliability Methods (FORM/SORM)
- Response surface methods
- Monte Carlo simulation using adaptive sampling
- Crude Monte Carlo simulation
The reliability analysis allows taking into account several loading cases as well as different boundary conditions using different failure functions.
- The definition of Failure functions is made using
- General functions
- Dependent on
- results (displacements, stresses, etc.)
- basic variables
- constant values
Results:
- Probability of failure for each limit state function,
- Parameter sensitivites of the limit state functions,
- Result sensitivities for basic variables (elasticities),
- Selected data of each iteration for Monte Carlo simulations.
Robust Design
In order to achieve a robust design, it is not sufficient to perform a simple optimization:
- Optimization often leads to reduced safety margins.
- The optimized design may have other critical parameters than the inital design.
- A 'reliable' optimum may be different than a deterministic one.
The proposed solution is a combination of optimization and reliability analysis.
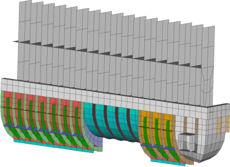
Optimization of water box with 18 design variables and 19 stochastic basic variables.
| Basic | Optimized | RDO | ||
| Mass: | M | 409 g | 315 g | 321 g |
| Failure probability: | Pf | 4.78 · 10-6 | 6.80 · 10-3 | 1.55 · 10-6 |
| Failure rate (one of): | 209 205 | 147 | 645 161 |