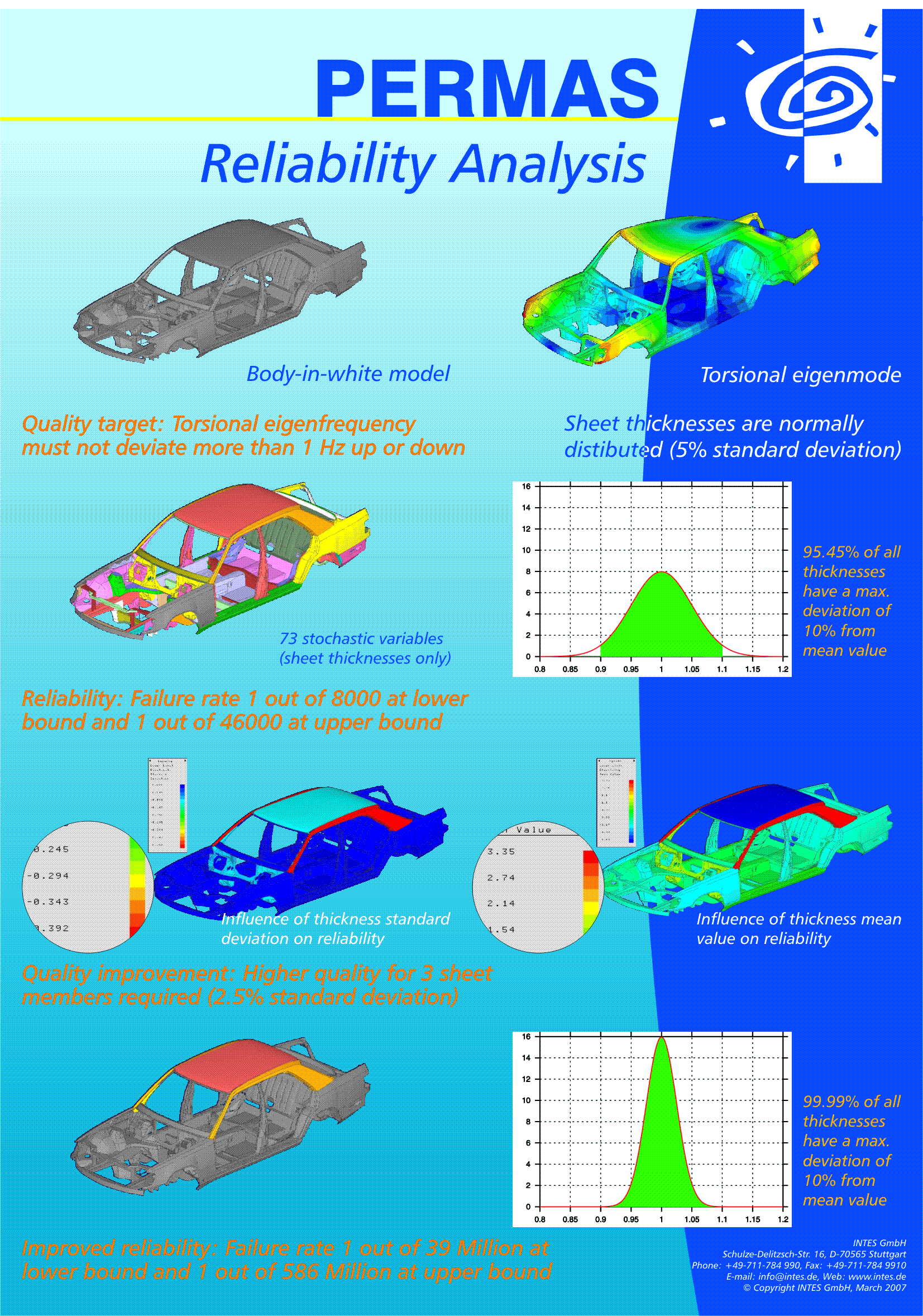
Zuverlässigkeitsanalyse/Robuste Design-Optimierun
Zuverlässigkeitsanalyse
Im Gegensatz zu dieser Methode trifft die stochastische Berechnung Annahmen über die Verteilungsfunktionen unsicherer Struktur- oder Lastparameter. Die zulässigen Grenzwerte für die Struktur sind zwar dieselben wie bei der deterministischen Analyse, aber die Ergebnisse umfassen dann die Versagenswahrscheinlichkeit in Bezug auf diese Grenzwerte sowie die Sensitivität dieser Versagenswahrscheinlichkeit in Bezug auf die unsicheren Parameter.
Dieses Modul verbindet die Finite Elemente Methode mit dem bewährten COMREL Programm der RCP GmbH in München. Auf diese Weise konnten die Erfahrungen aus beiden Software-Paketen für die Stochastische Finite-Elemente-Methode nutzbar gemacht werden.
Schritte einer Zuverlässigkeitsanalyse:
- Definition der unsicheren Größen der Strukturanalyse (wie Geometrie, Lasten usw.) über Basisvariablen, denen eine Verteilungsfunktion zugewiesen wird.
- Definition von Grenzzustandsfunktionen (oder Versagensfunktionen), die sich auf Ergebnisse einer Strukturanalyse beziehen.
- Berechnung der Versagenswahrscheinlichkeit für jede Grenzzustandsfunktion.
Basisvariablen:
- Designparameter (Geometrische Daten, Koordinaten)
- Lastfaktoren
- Materialparameter
- Parameter der Grenzzustandsfunktion
- Parameter anderer Basisvariablen
Dabei stehen mehr als 20 verschiedene Verteilungsfunktionen für die Beschreibung der unsicheren Variablen zur Verfügung.
Verfügbare Analyseoptionen:
- Lineare Statik
- Kontaktanalyse
- Dynamische Eigenwertberechnung
Verfügbare Methoden:
- Effiziente Lösungsverfahren mit Sensitivitäten als First/Second Order Reliability Methods (FORM/SORM)
- Response Surface Methoden
- Monte Carlo Simulation mit Adaptive Sampling
- Reine Monte Carlo Simulation
Bei der Zuverlässigkeitsanalyse können mehrere Lastfälle gleichzeitig berücksichtigt werden, genauso wie verschiedene kinematische Randbedingungen über verschiedene Versagensfunktionen.
- Die Definition der Versagensfunktionen erfolgt durch
- Allgemeine Funktionen
- Abhängig von
- Ergebnissen (Verschiebungen, Spannungen usw.)
- Basisvariablen
- konstanten Werten
Ergebnisse:
- Versagenswahrscheinlichkeit für jede Grenzzustandsfunktion,
- Parameterempfindlichkeit der Grenzzustandsfunktionen,
- Empfindlichkeiten des Ergebnisses in Abhängigkeit von den unsicheren Basisvariablen (Elastizitäten),
- Ausgewählte Daten für jede Iteration bei Monte Carlo Simulationen.
Robuster Entwurf
Um einen robusten Entwurf zu bekommen, genügt es nicht, nur eine einfache Optimierung durchzuführen:
- Optimierung führt oftmals zu reduzierten Sicherheitmargen.
- Der optimierte Entwurf kann andere kritische Parameter haben als der Ausgangsentwurf.
- Ein 'zuverlässiges' Optimum kann sich von einem deterministischen unterscheiden.
Die vorgeschlagene Lösung besteht in einer Kombination von Optimierung und Zuverlässigkeitsanalyse.
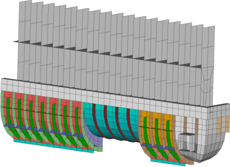
Optimierung Wasserkasten mit 18 Entwurfsvariablen und 19 stochastischen Basisvariablen.
| Basis | Optimiert | RDO | ||
| Masse: | M | 409 g | 315 g | 321 g |
| Versagenswahrscheinlichkeit: | Pf | 4.78 · 10-6 | 6.80 · 10-3 | 1.55 · 10-6 |
| Ausfallrate (eines von): | 209 205 | 147 | 645 161 |