Mit Dynamic Response Analysis kann die dynamische Antwort der Struktur im Zeit- oder Frequenzbereich ermittelt werden.

Die Lösung der dynamischen Gleichung kann dabei jeweils direkt (mit physikalischen Freiheitsgraden) oder modal (nach Transformation in den Modalraum) erfolgen.

• Die Antwort im Zeitbereich (Transient Response) wird durch Integration der Bewegungsgleichung ermittelt:
  • Transiente Antwort als absolute Antwort oder als rein elastische Antwort ohne Starrkörperanteil.
  • Direkte Integration der Bewegungsgleichungen oder Integration nach Transformation in den Modalraum. Als Löser stehen Newmark β und HHT (Hilber-Hughes-Taylor) zur Verfügung.
  Die Berücksichtigung konzentrierter nichtlinearer Struktureigenschaften ist möglich über
  • nichtlineare Federelemente,
  • nichtlineare Dämpferelemente und
  • nichtlineare Regelelemente.
• Die Antwort im Frequenzbereich (Frequency Response) wird durch Lösen des linearen, komplexen Gleichungssystems für jede geforderte Frequenz ermittelt:
  • Absolute Antwort oder als elastische Antwort ohne Starrkörperanteil.
  • Direkte Lösung des Gleichungssystems oder Lösung nach Transformation in den Modalraum.
• Frequenz- und drehzahlabhängige Steifigkeit und Dämpfung kann über das CONTROL6-Element berücksichtig werden.
• Ohne den Einschwingvorgang durchlaufen zu müssen, kann die stationäre Antwort (Steady-State Response) berechnet werden. Dabei werden Ergebnisse von Frequenzganganalysen im Zeitbereich überlagert. Dazu kann noch ein statischer Lastfall berücksichtigt werden. Dies ist für alle periodischen Anregungen mit bekannter harmonischer Zusammensetzung möglich.

Durch Angabe eines Knoten- oder Element-Sets kann bei der modalen Lösung die Ermittlung der Ergebnisse auf den angegebenen Bereich beschränkt werden. Diese Reduktion bringt eine enorme Einsparung an Rechenzeit und Plattenplatzbedarf.
Für die Antwort im Zeit- und Frequenzbereich gilt:

Verfügbare Dämpfungsmöglichkeiten

• Zur Modellierung der Dämpfungseigenschaften stehen folgende Möglichkeiten zur Verfügung:
  • Materialdämpfung bzw. Strukturdämpfung für Elemente,
  • globale Strukturdämpfung für Komponenten,
  • proportionale Dämpfung (Rayleighdämpfung),
  • viskose Dämpferelemente,
  • modale viskose Dämpfung,
  • modale Strukturdämpfung,
  • modale Struktur- und Rayleigh-Dämpfung für Teilkomponenten,
  • direkte Eingabe der modalen Dämpfungsmatrix.
  • direkte Eingabe der Dämpfungsmatrix
  Für die Berechnungen im Frequenzbereich können die Strukturdämpfungen wahlweise auch in Abhängigkeit der Frequenz beschrieben werden. Frequenzabhängige viskose Dämpfung ist mit Hilfe eines speziellen Elements (d.i. CONTROL6-Element) möglich.

 

Lasten

• Die Anregung erfolgt über statische Lastverteilungen, die mit zeit- bzw. frequenzabhängigen Funktionen kombiniert werden. Die Lastverteilungen können folgende Anteile enthalten:
  • Einzelkräfte oder -momente,
  • Verteilte Lasten (Linienlasten, Flächenlasten, Volumenlasten),
  • Trägheitslasten,
  • Vorgeschriebene Verschiebungen.

 

Ergebnisse

• Als Primärergebnisse werden
  • Verschiebungen,
  • Geschwindigkeiten und
  • Beschleunigungen.
  geliefert. Diese können als Funktion der Zeit bzw. der Frequenz zur Erstellung von xy-Graphen ausgegeben werden.
• Weiter lassen sich folgende Ergebnisse ableiten:
  • Reaktionskräfte,
  • Spannungen bzw. Elementkräfte,
  • Dehnungsenergien,
  • kinetische Energien,
  • spezifische Schallabstrahlungsleistung.

 

Weiter Funktionen für modale Methodem

Statische Verschiebungsformen können erstellt werden, um die modale Basis der dynamischen Eigenformen zu ergänzen. Damit verbunden sind zwei Vorteile:

• Im niedrigen Frequenzbereich werden dadurch die Ergebnisse wesentlich genauer.
• Es lassen sich auch Freiheitsgrade berücksichtigen, die nicht mit der Struktur selbst verbunden sind (z.B. bei Regelelementen).

Die statischen Verschiebungsformen können also durch folgende Angaben spezifiziert werden:

• direkt durch Knotenverschiebungen,
• durch externe Lasten,
• durch Ergebnisse einer anderen Analyse,
• durch natürliche Kräfte spezifizierter Elemente (wie Federkräfte),
• Implizit durch vorhandene Regelelemente.

Verbundene Situationen (Assembled Situations) können verwendet werden, um Frequenzganganaylsen mit verschiedenen dynamischen Lastfällen deutlich schneller zu berechnen. Anstatt die Lösung für alle Lastfälle getrennt durchzuführen, wird eine kombinierte Analyse erstellt.

Für die weitere Bearbeitung von modalen Ergebnissen stehen zusätzliche Hilfsmittel zur Verfügung:

• Zur Bewertung der Anteile von Moden an der Strukturantwort können die modalen Anteilsfaktoren für die Primärergebnisse ausgegeben werden.
• Zur Bewertung der Anteile eines Freiheitsgrades an der Strukturantwort können modale Beteiligungsfaktoren von Knoten für die Primärergebnisse ermittelt und ausgegeben werden.
• Für die Antwort im Zeitbereich kann über den betrachteten Zeitbereich eine statistische Auswertung der Spannungen und Schnittkräfte erfolgen, welche die Maximal- und Effektivwerte ermittelt. Diese statistischen Werte können z.B. für eine Lebensdauerbetrachtung herangezogen werden.

Kipper, Daimler AG

Die Harmonic Balance Methode (HBM) berechnet stationäres Antwortverhalten für nichtlineare Differentialgleichungen. In PERMAS wird es im Kontext einer nichtlinearen Frequenzganganalyse benützt. Mit der Funktion werden neue Anwendungsklassen ermöglicht, wie:

• Rasselgeräusche,
• Quietschgeräusche,
• Schraubverbindungen und Reibung zwischen Bauteilen,
• Fragen von Schwingungseinwirkung,
• Blattspitzen/Gehäuse Kontaktprobleme,
• Mehrfreiheitsgradsysteme (MDOF) und FE Modelle mit lokalen Nichtlinearitäten.

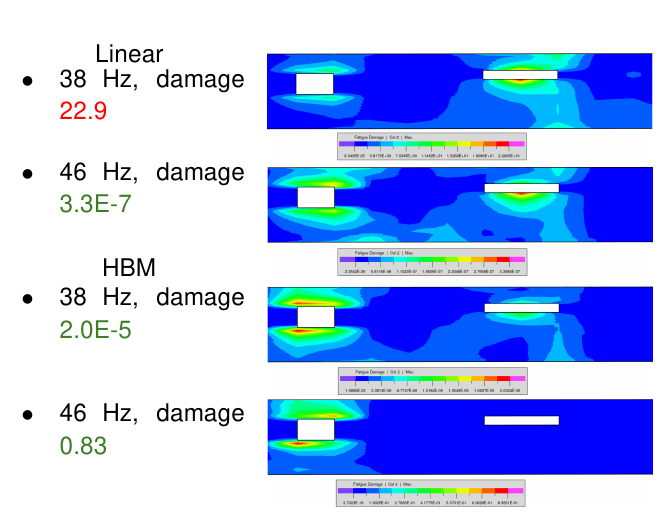
HBM+Lebensdauer

Häufig sind Schwingungsbeanspruchungen nicht vorhersagbar, man denke nur an ein Fahrzeug auf holpriger Straße, ein Gebäude unter Windlast oder ein Schiff in rauher See.

Solche zufälligen Lasten lassen sich zweckmäßig durch Zufallsprozesse im Zeitbereich beschreiben. Korrelationen zwischen diesen Prozessen und deren Transformation in den Frequenzbereich führen auf den zentralen Begriff der Spektraldichte (oder Power Spectral Density).

Unter dem bekannten weißen Rauschen wird hierbei verstanden, wenn die Spektraldichte einer Last über den gesamten Frequenzbereich einen konstanten Wert hat.

Die Lastgrößen werden als Spektraldichten spezifiziert und die Ergebnisse stehen als Spektraldichten oder RMS-Werte zur Verfügung.

Dieses Verfahren ist in modaler Form implementiert, d.h. zunächst wird ein Eigenwertproblem gelöst, dann werden die Schwingungsanregungen im Modalraum ermittelt und abschließend nach der Rücktransformation werden die Ergebnisse ausgegeben.

Bei einer Anregung des Untergrundes, wie bei einem Erdbeben, wird die dynamische Antwort im Zeitbereich durch ein vereinfachtes Verfahren ersetzt, das Abschätzungen für die Maximalwerte liefert. Die Voraussetzungen hierfür sind:

• unidirektionale Translationsbewegungen des Untergrunds,
• keine weiteren Lasten,
• Behandlung im Modalraum möglich,
• nur modale viskose Dämpfung.

Nach der Festlegung der Richtung der vorgeschriebenen Bewegung wird die Last als Spektrum der transienten Anregung (Responsespektrum) eingegeben. Auf dieser Basis wird folgender Berechnungsgang durchgeführt:

• Berechnung aller Eigenfrequenzen bis zur höchsten interessierenden Frequenz.
• Berechnung der maximalen Beiträge jeder Eigenform.
• Summation der maximalen Beiträge jeder Eigenform. Dabei stehen 7 verschiedene Summationsregeln für den Anwender zur Verfügung (wie CQC oder 10%-Regel).
• Ausgabe der Spitzenwerte.