Laminate Analysis
Usually the laminate is defined ply by ply. Each ply refers to a homogeneous and anisotropic material (frequently defined as orthotropic material) with a given thickness and a ply direction denoting the deviation angle from the material reference system. This definition is supported by VisPER. The homogenization then takes place in PERMAS following the Extended Laminate Theory (ELT).
In rare cases the homogenization may have been done outside of PERMAS. In this case the A, B, D and G matrices ABDG matrices may be input directly.
Beside linear analysis, also nonlinear analysis like buckling is supported (see PERMAS-NLS).
Primary analysis results are element forces, from which the layer stresses and strains are derived. These values are available in the middle of each layer. If one wants to get the stress values between two layers, then a layer with zero thickness may be introduced.
For the further processing of the stresses, a number of ply failure criteria are available. Beside Hoffman and Tsai-Wu criteria, such criteria can also be specified by user subroutines.
Laminate optimization
For laminate structures Free Sizing may be used in order to get ply shapes from the optimized thickness distributions. This reflects the fact that for a ply stack under given fiber angles not all plies are needed over the entire structure to bear the loads. The result will specify the element sets which need to have a certain ply of the ply stack.
Sizing of laminates is supported, where ply thicknesses and angles are to be optimized. Ply failure criteria may be used as constraints for the laminate sizing optimization. See laminate optimization
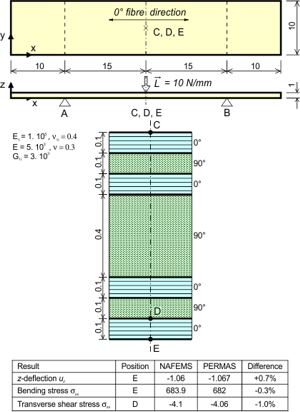
Laminate analysis of a NAFEMS test case.
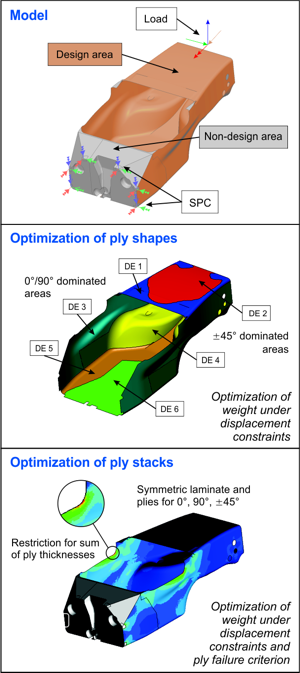
Two-step optimization of a monocoque.